Last week, in Number Sense 042, Awkward Goat and Billy Goat Gruff discovered that clock arithmetic was closed under addition, all sums were included in the original set of numbers. So far, clock addition has proved to have closure and an identity element in common with ordinary addition. Our intrepid Capra aegagrus hirci continue their search for more common properties.

“What the hell is a Capra agragus whatsit?” complained Billy Goat Gruff.
“That's us,” replied Awkward Goat. “Domestic goats. You and me.”
“Humph. Call a thing by its proper name is what I say,” said Billy Goat Gruff.

“Well, then, let's see whether clock addition is commutative and associative,” said Awkward Goat.
“Refresh my memory,” asked Billy Goat Gruff.
“Commutative means the order we add numbers doesn't matter. 1 + 2 is the same as 2 + 1.”
“The way I read our addition table,” said Billy Goat Gruff, “is the number on the left is added to the number on top. So 1 + 2 is 3, and 2 + 1 is also 3. So it seems to work, but do we have to check them all to prove it?”
“I think there might be an easier way,” replied Awkward Goat. “In our addition table, the sum of 1+2, and the sum of 2+1 are on a diagonal.”
“I see that,” said Billy Goat Gruff, “and the sums on that diagonal are all 3s. Not only that, but another diagonal is all 4s, another all 2s, and so on.”
“Good observation, Billy Goat Gruff,” said Awkward Goat, “and that means if we cut the addition table in half along a diagonal running through 0 + 0, 1 + 1, 2 + 2, 3 + 3 and 4 + 4, we get two triangles which are mirror images of each other.”
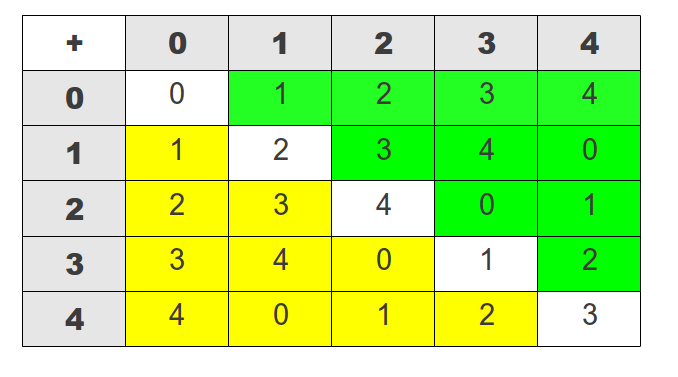
“Why would we want to cut our table in half?”
“Well, because of the way we put the table together, if we take any pair of numbers to add, the sum will be in one triangle. But if we reverse the order of those numbers, we'll get the sum in the mirror image spot in the other triangle.”
“And since the same number is in that spot, reversing the number gives us the same sum,” concluded Billy Goat Gruff.
“Alright,” he continued, “clock addition is... what did you call it?”
“Commutative”
“...commutative,” said Billy Goat Gruff. “I suppose ordinary addition is commutative as well.”
“Yes,” said Awkward Goat, “yes it is. We have yet another common property. This is fun!”
“I'm glad you think so,” said Billy Goat Gruff. “What's next?”
“The associative property,” replied Awkward Goat. “When there are more than two numbers to add, we can group the numbers in any way we want, and still get the same sum.”
“Group the numbers?”
“Well, our addition table only handles pairs of numbers,” explained Awkward Goat. “So if we have three numbers, say, we can add the first two first then add the last one to that sum, or, we can add the last two first then add the first number to that sum, and we'll get the same sum both times.”
“You're either going to have to talk slower,” said Billy Goat Gruff, “or give me an example.”
“An example, then,” said Awkward Goat. “ 1 + 2 + 3. You can add 1 + 2, get 3, then add 3 to that to get 6. So (1 + 2) + 3 = 6.”
“So far, so good.”
“You could also add 2 + 3 first, and get 5. Then you add 1 + 5 to get 6 again. 1 + (2 + 3) = 6”
“I see,” said Billy Goat Gruff. “Yes, I do see! And I think I can prove it!”
“Be my guest,” invited Awkward Goat.
“Alright then,” said Billy Goat Gruff. “We have three numbers, doesn't matter which they are... so let's just call them the red number, the yellow number and the green number.”

“Now, if we add these in order, we would add red and yellow, get a sum, then add green to that sum.”
“With you so far.”
“But our commutative property says we can switch red and yellow and get the same answer.”

“OK.”
“And the commutative property says we can switch the red and green number and still get the same sum.”

“Alright.”
“So if we add these, in order, we would add yellow and green, then add red. But according to the commutative property the sum would be the same as it was before we started moving numbers around.”
“Makes sense to me, Billy Goat Gruff,” said Awkward Goat. “We'll make a mathematician of you yet!”
“I'm not sure that's a compliment, Awkward Goat, but thanks anyway.”

Have fun in the comments


