Last week, in Number Sense 044, Awkward Goat and Billy Goat Gruff invented a new operation, called Butts, which worked with three colors, Red, Yellow and Green. Butts has an identity element, Yellow, and is commutative. The jury is still out on whether Butts is associative or not.
“Well,” said Billy Goat Gruff, “we certainly found out how not to go about proving Butts is associative. But how do we find out whether it is or not?”

“Since we only have three colors in our table,” said Awkward Goat, “there are only six possible combinations using all three colors. We can check them all.”

“Since Yellow is the identity element,” said Awkward Goat, “anywhere we have Yellow butting another color, or another color butting Yellow, we can simply remove the Yellow square and leave the other color.”

“That makes our job a lot simpler,” said Billy Goat Gruff. “and they are all Red butts Green or Green butts Red.”
“And, according to our Butt table, both those give us Yellow.”

“Two of them are obviously the same thing,” said Billy Goat Gruff, “once we remove the parentheses. Red butts Green equals Red butts Green. And the other way around, too.”
“Let's remove the parentheses, first,” said Awkward Goat.
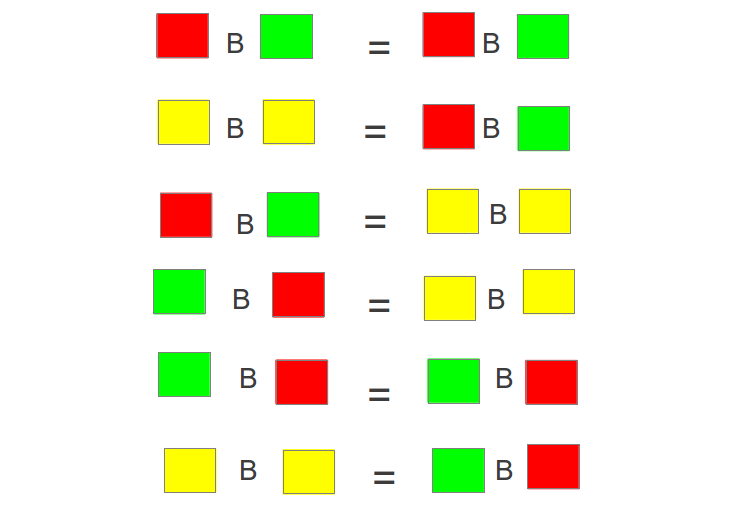
“So,” said Billy Goat Gruff, “we have Red butts Green, Yellow butts Yellow, and Green butts Red. According to our table, Red butts Green is Yellow.”
“Yellow butts Yellow is Yellow,” said Awkward Goat, “since it's the identity element.”
“And Green butts Red,” continued Billy Goat Gruff, “is Yellow.”
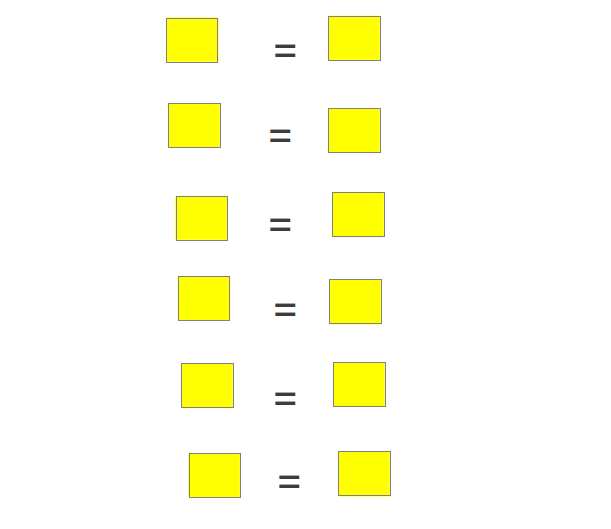
“I did not see that one coming,” said Billy Goat Gruff. “Does this mean our Butting operation is associative?”
“Not yet,” said Awkward Goat, “because we might have a situation where we have two Red and one other color.”
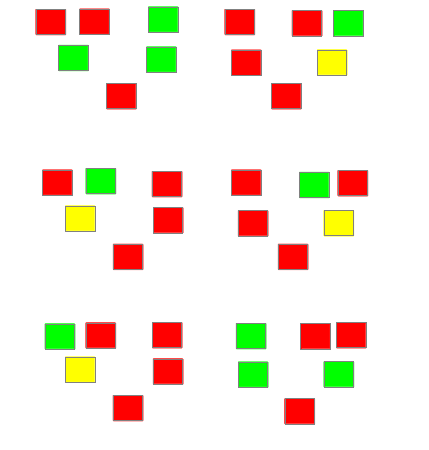
“If we have two Reds and a Green, anywhere we put the Green, the answer is the same: Red. We'll get a similar result for two Greens and a Red: we'll get Green.”
“What about two Reds and a Yellow?” asked Billy Goat Gruff.
“The Yellow cancels itself out,” said Awkward Goat, “since it doesn't change the other color. So two Reds and a Yellow winds up becoming Red butts Red is Green, however you associate it. The same would be true for two Greens and a Yellow giving Red. If you have two Yellows, though, you end up with the third color, even if the third color is Yellow.”
“What's left?” asked Billy Goat Gruff.
“Three of a kind,” answered Awkward Goat. “Three Reds, let's see, Red butts Red is Green, and Green butts Red is Yellow. Three Greens: Green butts Green is Red, and Red butts Green is Yellow. And of course, three Yellows will give Yellow.”
So it seems association works for our Butt operation,” said Billy Goat Gruff. “I can't think of any other combinations we might try, and all the combinations we've looked at so far we can combine in any order.”
“So, let's sum up,” said Awkward Goat. “We have an operation, Butt, which works on three colors, Red, Yellow and Green.”
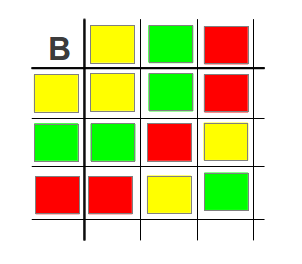
“Butt is closed. Every combination gives back one of the original colors as a result.”
“Butt has an identity element, Yellow, which gives back the color it butts, or the color that butts it.”
“Butt elements have inverses.”
“Excuse me, Awkward Goat,” said Billy Goat Gruff. “What's an inverse?”
“I'm sorry, I thought I explained that,” apologized Awkward Goat. “No? Well, if there is a color that results in Yellow, the identity element, when it is butted, then that color is the butting color's inverse. For example, Red butts Green gives Yellow, so Green is Red's inverse.”
“So Red is Green's inverse?” asked Billy Goat Gruff.
“Exactly!”
“Then what is Yellow's inverse?” asked Billy Goat Gruff. “It can't be Red or Green, because we don't get Yellow as a result.”
“That's true, but Yellow is its own inverse,” said Awkward Goat. “Yellow butts Yellow gives Yellow. Remember, inverse doesn't mean it changes a color to Yellow, it just means the result is Yellow.”
“I see. Carry on,” said Billy Goat Gruff.
“And finally, Butt is associative,” finished Awkward Goat. “I think we have a Group.”
“A Group?” asked Billy Goat Gruff.
“A Group,” replied Awkward Goat. “A set of elements, Red, Yellow and Green, with an operator, Butt, that is closed, has an identity element, all its elements have inverses, and is associative.”
“The idea,” mused Billy Goat Gruff, “that a bunch of colors, running around in a fenced in yard, butting each other to make more of the same colors, is mathematics... well, let's just say it all seems rather abstract to me.”
“Excellent!” cheered Awkward Goat, “You've got it!”

Have fun in the comments.


