In my research into wage trends, I stumbled upon another indication of growing inequality in America. I found a trend toward an increase in the difference between what super-earners are making and what the rest of us are making. By super-earners, I'm not talking about Wall Street private-equity sharks who disguise their earnings as capital gains, or others who get capital-gains income. I'm talking about those who earn wages and salaries.
Yes, even among those of us who work for The Man, there's a growing pay gap. I'll explain how I discovered this below the mighty squiggle.
I am a writer-researcher in the field of career information. For a blog I was researching, I was trying to identify occupations that have a few superstars. You're familiar with superstar chefs such as Emeril Lagasse, superstar doctors such as Sanjay Gupta, and superstar teachers such as Salman Khan. I was wondering which occupations have the greatest distortion of their earnings distribution, with a few extremely high earners leaving the rest in the dust.
The method I used was to compare the figures for the mean and median earnings in each occupation surveyed by the Department of Labor. The mean is the algebraic average, so if the mean is a lot higher than the median, it means that a few star earners are pulling up the average. (They are doing the same thing that high-achieving students do to grades when they “ruin the curve” for average students.)
Here is an example that explains what I was doing. Let’s say I’m looking at an occupation with only seven workers, and this is how their earnings are distributed:
Worker Annual Earnings
A $10,000
B $20,000
C $30,000
D $40,000 (median: half earn more than D, half less)
E $50,000
F $60,000
G $70,000
The median wage is $40,000, and if you do the math you’ll find that $40,000 is also the mean (average) wage. That makes sense because the wages are distributed very evenly here. But let’s say that worker G suddenly becomes a star and earns $400,000. The median does not change, but the mean now soars to $87,143. (That’s a difference of 118 percent.) Having a star earner in the mix of workers creates a big gap between the median and the mean.
Using figures reported on in the Occupational Employment Statistics (OES) estimates for May 2011, I calculated the difference between mean and median in terms of the percentage of the median. The following list consists of those occupations with a difference greater than 25 percent.

Of the occupations on the list, some are in the fields of entertainment, sports, or media, where you expect superstars to emerge. But you may be surprised by the business occupations that made the list. The reason becomes clear once you consider an occupation that straddles the field of business and also the aforementioned fields: Agents and Business Managers of Artists, Performers, and Athletes. A few agencies represent millionaire athletes and are able to pay their agents outstanding salaries, but most agencies represent clients with much more modest earnings. Something similar is true for Real Estate Brokers and Real Estate Sales Agents. Their earnings are based on a percentage of the price of the properties they sell, so those who handle expensive homes and high-ticket commercial properties earn sky-high commissions. Three more examples are Securities, Commodities, and Financial Services Sales Agents; Insurance Sales Agents; and Personal Financial Advisors.
Okay, none of this surprised me. What did strike me was noticing that the average difference (between median and mean) for all workers in all occupations is as high as 31 percent. Note that only 14 occupations have so large a difference.
To help understand this earnings gap, I dug up data from OES surveys going back to 2001, the earliest year for which I was able to obtain mean and median figures for all jobs in all occupations. Here is the graph I generated.

You’ll notice that although both lines slope upward with the general modest inflation of wages, the mean increases at a faster rate, causing the gap between them to grow larger. Here is a graph of how that difference changes over those same years.
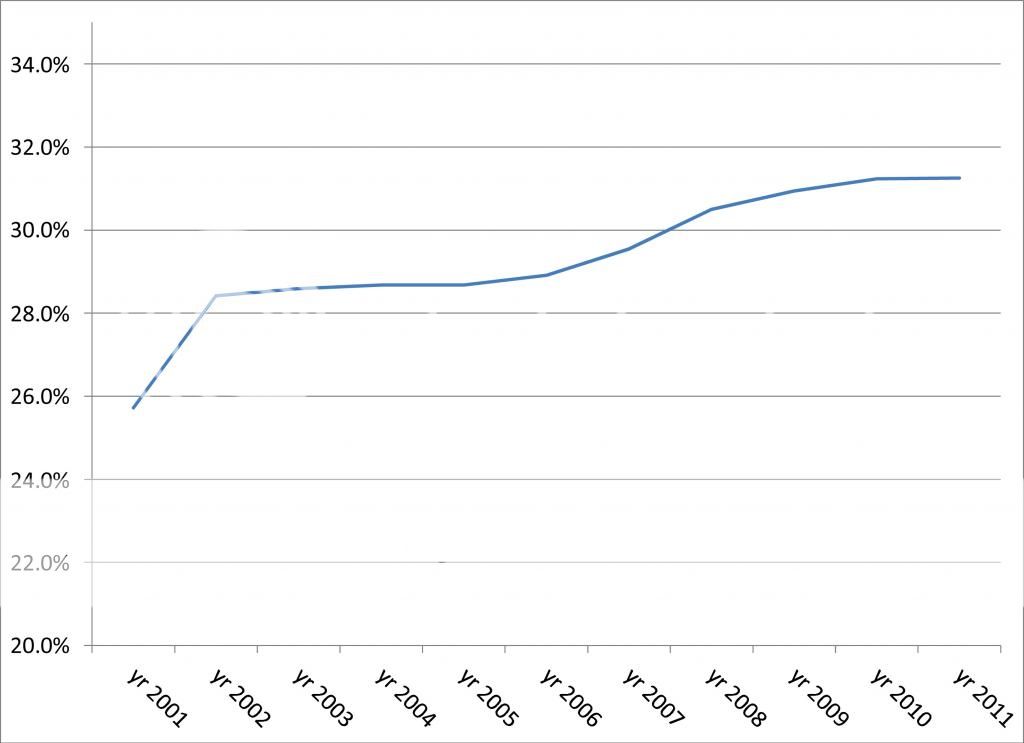
This shows that the difference has grown by 6 percent in the past 10 years. The present 31 percent difference is yet one more measure of the growing inequality in earnings that marks our present era as another Gilded Age. And, mind you, this difference is based solely on wages and salaries; it does not include the superstar earnings of those who are self-employed or whose earnings are disguised as capital gains.


