This year's Nobel prize in Chemistry will be awarded to Israeli scientist Daniel Shechtman for his discovery of quasicrystals, metallic alloys with atoms arranged in orderly, infinite, aperiodic, crystal-like patterns with theoretically forbidden (typically 5 fold) symmetry. This form of matter was believed to be impossible to create. Schectman made his discovery while on sabbatical at the U.S. National Bureau of Standards April 8, 1982 . He was laughed at.
"I told everyone who was ready to listen that I had material with pentagonal symmetry. People just laughed at me,"
When he returned home, Shectman was kicked out of his university research group but found a new group. He then moved to Israel where he found someone he could publish with, but his paper was rejected. He got it published on the second try, but his results were mocked and derided. Double Nobel winner Linus Pauling said
"Danny Shechtman is talking nonsense. There is no such thing as quasicrystals, only quasi-scientists."
Today, Dr Shectman is preparing to receive the Nobel prize.
A quasicrystal of silver aluminum similar to the first quasicrystal of magnesium aluminum discovered by Nobel prizewinner Daniel Shechtman. Photograph: Wikimedia Commons
What is a quasicrystal?
The long answer is: no one is sure. But the short answer is straightforward: a quasicrystal is a crystal with forbidden symmetry. Forbidden, that is, by “The Crystallographic Restriction”, a theorem that confines the rotational symmetries of translation lattices in two and three-dimensional Euclidean space to orders 2, 3, 4, and 6. This bedrock of theoretical solid-state science—the impossibility of five-fold symmetry in crystals can be traced, in the mineralogical literature, back to 1801—crumbled in 1984 when Dany Shechtman, a materials scientist working at what is now the National Institute of Standards and Technology, synthesized aluminium-manganese crystals with icosahedral symmetry.
The term “quasicrystal”, hastily coined to label such theretofore unthinkable objects, suggests the confusions that Shechtman’s discovery sowed. What’s “quasi” about them? Are they sort-of-but-not-quite crystals? Solids with some sort of quasiperiodic structures? For that matter, what is a crystal?
Since the discovery of x-ray diffraction in 1912, a crystal’s identifying signature has been sharp bright spots in its diffraction pattern; that’s how Shechtman knew his were special. If it looks like a duck and quacks like a duck, it’s a duck: charged in 1992 with
formulating a suitably inclusive definition, the International Union for Crystallography’s newly-formed Commission on Aperiodic Crystals decreed a crystal to be “any solid having an essentially discrete diffraction diagram.” In the special case that “three dimensional lattice periodicity can be considered to be absent,” the crystal is aperiodic (http://www.iucr.org/...).
X ray diffraction pattern of a quasicrystal
The modern mathematics that applies to quasicrystals was developed by British mathemitician Roger Penrose in the 1970's based on inspiration from tilings done by Johannes Kepler.
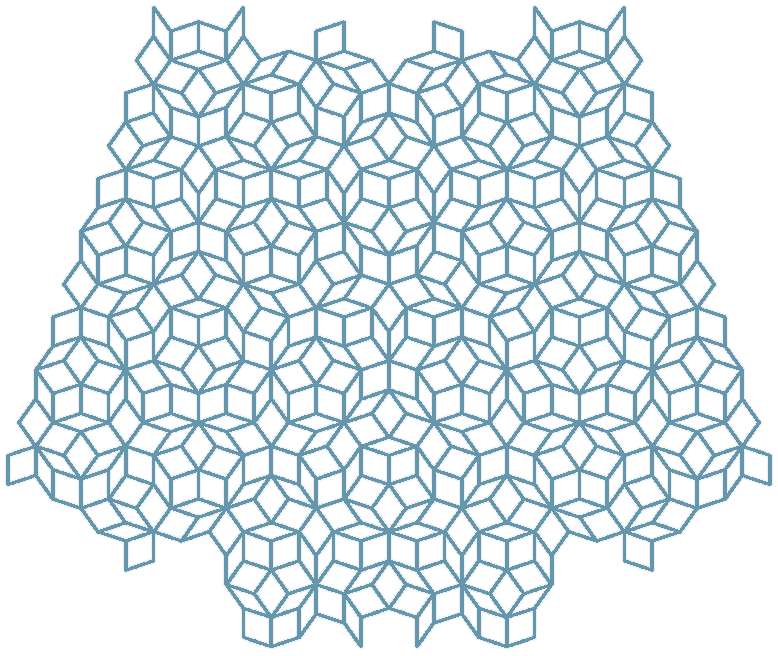
Penrose tiling that produced the X-ray diffraction pattern above.
However, Islamic mathematicians and artists discovered the "Penrose tilings" of quasicrystals hundreds of years before Kepler.
Quasicrystal type pattern in decagonal strapwork above an arch in the Abbasid al-Mustansiriyya Madrasa in Baghdad, Iraq, which dates to between 1227 and 1234.
Around 830, the Persian mathematician Muhammad ibn Musa al-Khwarizmi made a mathematical breakthrough: He incorporated Euclid’s geometry into a unifying theory that became known as algebra (from the Arabic jabara). This spawned a wave of new mathematical ideas expounded by al-Khwarizmi’s successors over the next centuries. The flowering of scientific brilliance from the ninth to about the 13th century—a period often described as the “golden age” of Islamic science—was promoted by the patronage of Muslim rulers and the intellectually stimulating atmosphere in their capitals. Scholars from all over the Islamic world gathered in cities such as Baghdad, Cairo and Córdoba to exchange ideas, peruse the great libraries and make names for themselves.
DAVID JAMES: QUR’ANS OF THE MAMLUKS (THAMES & HUDSON)
A decagon, surrounded by bowties and hexagons, forms the basis of this cover of a Mamluk copy of the Qur’an that dates to the early 14th century.
Not all of them were Muslims—many Jews, Christians and Zoroastrians made important contributions—nor did they all write in Arabic: Persian in particular remained an important lingua franca for scholars from different backgrounds. Neither did these scholars limit their research to the works of the ancient Greeks. As the Islamic world expanded, it drew in scientific knowledge from the civilizations with which it came into contact, especially India and China. For example, mathematics benefited immensely from the adoption of the ancient Indian positional number system, in which the lowest-value digit is on the right (as in “25,” where the five represents how many ones are in the number and the two represents how many 10’s) and which includes the concept of “zero,” the empty position. Muslim mathematicians adopted Indian numerals around the early ninth century: A few years before his famous book on algebra, al-Khwarizmi wrote a work entitled On Calculation with Hindu Numerals. The introduction of the Hindu–Arabic numeral system to Europe in the early 13th century is credited to Leonardo of Pisa (known as Fibonacci), who is thought to have learned about it from Muslims in North Africa. Like that system, many other mathematical concepts preserved or developed by Muslim mathematicians found their way north, providing the foundations for a reinvigoration of the sciences in Europe.
Peter J. Lu, a physics graduate student at Harvard University, noticed a striking similarity between certain medieval mosque mosaics and a geometric pattern known as a quasi crystal—an infinite tiling pattern that doesn’t regularly repeat itself and has symmetries not found in normal crystals (see video below). Lu teamed up with physicist Paul Steinhardt of Princeton University to test the similarity: If the patterns repeated when extended infinitely, they couldn’t be true quasi crystals.
On this panel in the Shah Mosque in Isfahan, Iran, ten-pointed stars—none of them shown completely —anchor the edges of a pattern in which four of the five girih shapes can be found. Both the stars and the scallop-edged hexagons are placed according to an underlying design of still more decagons and pentagons. The stars’ incompleteness reminds the viewer that the pattern actually extends into infinity.
Most of the patterns examined failed the test, but one passed: a pattern found in the Darb-i Imam shrine (seen in the image above), built in 1453 in Isfahan, Iran. Not only does it never repeat when infinitely extended, its pattern maps onto Penrose tiles—components for making quasi crystals discovered by Oxford University mathematician Roger Penrose in the 1970s—in a way that is consistent with the quasi crystal pattern.
The quasicrystalline structured tilings were used by religious mystics, including Sufis, to contemplate infinity.
Girih pattern of a decorated arch in the Sultan’s Loge of the Ottoman-era Green Mosque in Bursa, Turkey, which was completed in 1424. The girih tiles make possible large-scale patterns because each edge has the same length, allowing different combinations to be aligned. What is more, every edge is intersected at its midpoint by two decorating lines at fixed angles, which ensures that the lines continue across the edges from one tile onto another. A further innovation was achieved by dividing girih tiles into smaller ones to create overlaid patterns at two different scales, a method mathematicians call “self-similarity transformation.” This kind of subdivision, combined with the symmetry imposed by the shapes of the girih tiles, creates non-periodic tiling, just like the Penrose patterns.
Remarkable Properties of Penrose Tilings
The most remarkable property of Penrose Tilings is that every finite portion of any tiling is contained infinitely often in every other tiling. This, of course, is true of all periodic tilings, but it's not at all obvious that it should be true of a non-periodic tiling. This property has several consequences:
• No finite patch of tiles can force a tiling (determine the rest of the tiling).
• It is impossible to tell from any patch of tile which tiling it is on.
• Only at their infinite limits are the different patterns distinguishable. A finite patch of an Infinite Star pattern might only be a local piece of some other pattern, but there is also an Infinite Star pattern that has five-fold symmetry to infinity. Only if you know the characteristics of the pattern to infinity can you tell.
Wrapping a column in the early–19th-century Tash Hauli palace in Khiva, Uzbekistan, a strapwork pattern of decagons and pentagons is filled with vegetal arabesques that maintain five-fold and ten-fold symmetry.
In 2009, quasicrystals were discovered in nature.
Rock sample bearing the mineral khatyrkite that shows 5 fold quasicrystalline symmetry. The lighter-colored material on the exterior contains a mixture of spinel, augite, and olivine. The dark material consists predominantly of khatyrkite (CuAl2) and cupalite (CuAl) but also includes granules with the composition Al63Cu24Fe13. The diffraction patternswere obtained from the thin region of this granule indicated by the red dashed circle, an area 0.1 μm across. The inverted Fourier transform of the HRTEM image taken from a subregion about 15 nm across displays a homogeneous, quasiperiodically ordered, fivefold symmetric, real space pattern characteristic of quasicrystals.
The fivefold (A), threefold (B), and twofold (C) diffraction patterns obtained from a region (red dashed circle) of the granule in Fig. 1B match those predicted for a FCI quasicrystal, as do the angles that separate the symmetry axes.
A nearly structurally perfect natural quasicrystal that formed under geologic conditions would have several implications for geology and condensed-matter physics. The definition of a mineral, which previously included periodic crystals, incommensurate structures (18, 19), and amorphous phases, would henceforth include quasicrystals, expanding the catalog of structures formed by nature and raising an interesting challenge to explain how they formed naturally.
